The architect at my work recently handed a prototype he build to me and I was instructed to maintain it. In so doing, I have found a nice little parable here about how things can go wrong and how it can spiral out of control. Also, let’s spit on Hibernate.
At the outset, he chose to build a REST server with Hibernate. He went with RESTEasy, which antedates Jersey (JAX-RS/JSR-339) by a few years. The first problem in our story happens because he is using an old version of RESTEasy and an older version of Hibernate. Namely, the JSON writing portion (Jackson) gets confused by the Hibernate proxies to the model objects he’s retrieving and he proceeds to annotate most of the Hibernate mapping with lazy="false".
We have seen in the past that this is a common source of pain because Hibernate actually has two settings here where it should have one. The setting lazy="false" tells Hibernate, you must immediately retrieve these properties. But, another setting (such as fetch="subselect") actually tells Hibernate how to do this, and without it, you get a nice combinatorial explosion of queries as Hibernate must iterate row by row running queries that lead to it iterating again running queries… a single web request can easily balloon into several hundred thousand queries. Also, there were no indexes, so these queries were running full table scans for essentially every foreign-key based retrieval.
The immediate problem of JSON not being generated is solved, but the “root cause” problem of many other issues is born. Now many of the requests are slow. The next stop is apparently Angular. The best way to avoid expensive work is to not do it, followed by caching the results. Now he introduces a significant caching layer in Angular, in the browser. He does this before implementing pagination.
New problem. Rendering time appears bloated. (I think this is conflated with fetch time.) Solution: angular link-time string concatenation rather than using ng-repeat which generates watches recursively. Rendering time improves. Code is much larger and more brittle.
New problem. Cached data is out-of-date. Solution: create a web socket and tie into Hibernate’s interceptor system to broadcast notifications whenever entities are persisted. Bunch of new code for handling notifications and updating the relevant caches.
The Hibernate-friendly solution to these problems is as follows:
- It’s possible to annotate the model classes to hide Hibernate proxy properties, so that Hibernate proxies can be converted to JSON, even with very old versions of Jackson and RESTeasy
- Remove the
lazy="false"or addfetch="subselect", depending on whether it is actually a performance improvement to fetch immediately - Replace generic fetches of objects with JQL queries using
INNER JOIN FETCHthat obtain exactly the entities needed at the time they are needed - Add foreign key indexes to the database, and others as-needed
- Delete the cache layer, since it may be hiding performance issues
- Delete the web socket notification layer, or make it induce a reload of the page rather than tinkering with cached values that may not even be displayed
However, I have a more holistic approach I would like to recommend, because the current scheme looks something like this:
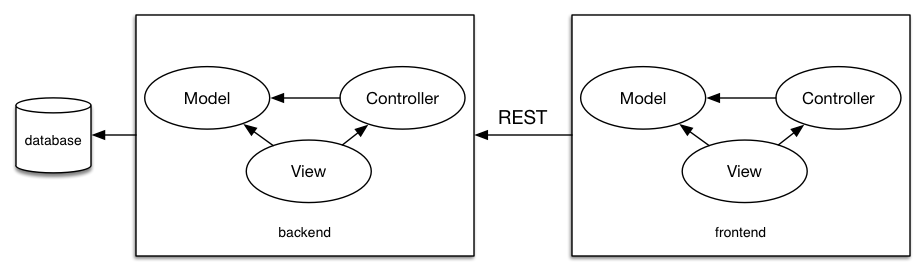 stupid model with lots of MVC
stupid model with lots of MVC
This is stupid. You’re doing a lot of changing the shape of data, but it’s you in the front-end, it’s you in the back-end and it’s you in the database. So just admit that the person wearing the front-end hat is the same person wearing the back-end hat and the person writing the database, and let each of these components do the part of their job they are good at:
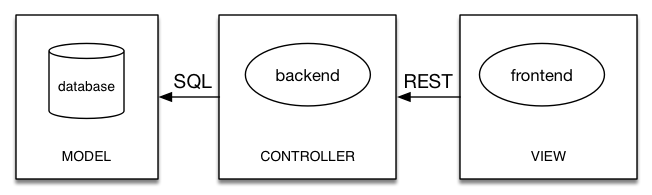 less stupid model with only one MVC
less stupid model with only one MVC
There. Now your back-end can be honest and have the SQL, yes SQL, it needs to build exactly the views that your front-end provides. Hibernate doesn’t need to be involved here because it isn’t buying you anything to take your fat objects out of the database at great cost, transmit them in all their bulk to the front-end, have them taking up space in the user’s browser (which is probably the worst at managing the memory) only to have your Angular front-end iterate through them and render four properties in a table view. You’re spending in the database, fetching stuff you don’t need, spending in the back end to convert it from one format to another, and then doing the same conversion again in the front-end. Caching is not the solution here! Doing less work is the solution! Build a holistic solution rather than three incomplete pieces of a solution!
So think holistically. Use mybatis and actually learn some SQL. Make the database do the work of changing the shape of the data—that’s what it’s for! Make the back-end do things to the data: this is what brings action and processing to your data. And then, make the front-end just show the damn data! That’s all it needs to do: display the information and collect the user’s desires for processing and pass it back. THIS IS AN MVC SYSTEM ALREADY—it doesn’t help to make the model MVC, the view MVC and the controller MVC!
In conclusion, Hibernate is garbage.
Addendum
I should make it clear I have the utmost respect for the architect. The high-level ideas in this program are great. Their execution is essentially befitting of a prototype. I don’t think I would have come up with as powerful, general or interesting of a design if left to my own devices.
This is adapted from a comment I left on Hacker News.
Why don’t we replace SQL with some other, better query language, perhaps something “equally powerful” like
get name, age -> (foos.id X bars.foo_id) |> get first(name) |> head?
Part of the point of SQL is that the database may choose to satisfy your query in a very different manner than you might expect given the procedural reading. The example query is a nice illustration; a modern relational database may move project/select steps earlier in the processing as long as it doesn’t change the declarative meaning. Doing this kind of rearranging with a pipeline-looking query language is going to surprise people because you’re giving the majority of people who think procedurally a false affordance.
Here’s a nice example of a false affordance from a blog I can’t read:
 false-affordance
false-affordance
The handles on the left doors give you a clue how they are to be used. ON the right, they’re mounted on the wrong side of the door so they will be awkward and surprising to use.
By the way, the false affordance is the fundamental cause of the object-relational impedance mismatch: the ORM is trying to put a low-level wrapper around a higher-level idea. OO languages are still row-by-row procedural systems where relational databases are set-oriented.
If the target language is Haskell or Ruby or another “sufficiently DSL-capable language” it will be possible to make an internal DSL that encapsulates your query. However, in that case I think users will be surprised when they have either non-obvious limits to how they can intermix query with in-language code, or else bad database performance compared to Postgres. You can see a little of both in the story of RethinkDB. If you are not using an internal DSL, you’ll be stuck in the same situation as SQL where you are embedding your query language in the code somehow.
Relational databases are not just storage technology with a complicated query language. They are also integration technology. SQL’s surface syntax may be unfortunate, but I’m increasingly doubtful that there is going to be a serious general-purpose database competitor that manages to hit the same notes only better. The main contender from the 90s was OODBs; they managed to have both shitty performance and lacked the ecosystem that makes SQL so useful as an integration technology: your application may be the main actor, but there are usually a large number of supporting cast members like cron jobs, reports, little scripts, ad-hoc queries, backup and restore etc, and having to do all of that with an OODB is very painful.
There are now and will continue to be niches where relational databases suffer, the prominent one today being distributed data storage. But the problem you think is a problem really isn’t a problem. Industrially speaking, “I don’t like SQL” is a non-problem. For people who hate it, there are ORMs that make it possible to ignore it most of the time for better or worse (mostly worse, but whatever). Syntactically, the main problem with it is that different dialects that behave slightly differently. This turns into a major engineering annoyance, but one that is mostly swallowed by our library dependencies, who have by now already basically taken care of it.
The benefit of using a modern relational database (I’m talking about Postgres but it applies to SQL Server and probably others as well) is they already have hundreds or thousands of man-years of effort put into optimizing them. I really thought RethinkDB had a brilliant design and it was going to be the next generation database. But it performed worse than Postgres and that makes it basically a non-starter. This is part of why niche databases are not based on SQL: if you handle a niche well, I will tolerate your oddities, but if you want to build a new general-purpose database today, in 2018, you can’t just have a better design. Your better design has to come with better performance and the ecosystem, the tool support, maintainability, etc., or it’s a non-starter. Databases are one of the hardest technical markets to break into. For most companies, the data is actually the most important thing.
I got one of these things for Christmas from my wife’s family secret santa:
 Smokey Mountain Cooker 14”
Smokey Mountain Cooker 14”
The way this thing works is pretty interesting. At the bottom are some coals. You put wood on those coals, and they smoke. At the top is your food. In between is a bowl of water. The water acts as a moderator for temperature and as a humidifier.
So I’ve now smoked meat on this thing twice, in the dead of winter. The first time, I did a whole chicken, and it came out looking like this:
 smoked chicken
smoked chicken
I was a little intimidated at first, but I watched a bunch of videos and everything turned out great! I broke all the rules, looked at the food too many times (every half-hour the first time, every hour the second time), fussed with the coals too many times (well, once, the first day), bought and used the wrong charcoal (lump, should have just got the regular stuff) and the wrong wood (chips, should have got chunks), and it was still moist and delicious. Frankly, smoking is a lot easier than grilling!
If you have space, you should get one of these things. They’re easy to use. They take forever, but you really don’t have to screw around with them that much once you set them up.
Here’s my rub recipe: equal parts salt, sugar, cumin, garlic, oregano and New Mexican red chile powder. I admit I did use a dash or two of MSG (it’s fine, really) and some ground anise, but I don’t have the amount right. I think another equal part of it would be too sweet, but I did about a half portion of it and that wasn’t quite enough.
Anyway, it’s been very fun and I recommend you try it if you like smoked meat.
Reification is a concept that gets realized in programming in a handful of different ways.
1. Reification in RDF
In RDF, reification takes claims like “John is a tool” and adds in the contextual information about who is making the claim, turning them into claims like “Dave says John is a tool.” This is useful because RDF documents don’t have to have authority statements within them; if you obtain one from me, you may want the effect of reading it to be something like “Daniel says contents of daniel.rdf.” rather than just the contents of my file.
2. Reification in object-oriented terms
Often during the evolution of a program, a method winds up sort of taking over a class and acquiring a large number of parameters. Something like this:
class Plotter:
def plot_schedule(schedule): ...evolves into something a little worse like this:
class Plotter:
def plot_schedule(schedule, weather, program, authors, start, stop, ...):
...At some point you have to package up that whole method into an object, which will usually have the word “request” in the name, and then the method will take one of these requests instead of a billion parameters:
class Plotter:
def plot_schedule(schedule_request):
...
class ScheduleRequest:
def set_schedule(schedule): ...
def set_weather(weather): ...What’s happened here is that the arguments to plot_schedule have been reified into an object called ScheduleRequest. The process could be taken as far as moving the actual plot method onto the schedule request. Maybe the plotter should just have lower-level methods anyway, and then ScheduleRequest becomes something more specific like SchedulePlot.
In general, converting verbs into nouns is a kind of reification.
In the previous article, the discussion of lambda calculus is a bit misleading. We’re not using lambda calculus terms as the intermediate representation. We’re being inspired by the lambda calculus and aping it as a mechanism for propagating information around in the intermediate representation.
In Python, using the SQLAlchemy, you can construct conditions by using expressions like Users.t.name == 'bob'. The object in Users.t.name is some kind of column type, and it overloads __eq__ in such a way that when you evaluate it against ‘bob’, rather than returning a boolean truth value, it returns some kind of filter expression object. This is a way of delaying binding: nothing is really computed at this moment, it’s just all bound together in preparation for a later evaluation step. In the case of SQLAlchemy, that evaluation is actually going to generate part of an SQL query. This gives the appearance of a bridge between Python and SQL.
What’s really happening in a DCG statement like sentence(VP) --> np(NP), vp(NP^VP) is a beautiful confluence of Prolog ideas. Prolog’s unification is used not just as pattern matching against the structure of the subterm result from the verb phrase, but also to propagate the value from the noun phrase into the verb phrase. Because unification is more like forming a link than procedurally assigning variables, we can unify things in any order. This is how we get a noun from before the verb and a noun from after the verb to live nicely side-by-side inside a term build by the verb.
We didn’t really wind up having to build anything like the lambda calculus, because binding in LC is just like binding in Prolog. In fact, we got a “rename” step “for free” because Prolog variable names are not global.
So where was the lambda calculus? It wasn’t in the AST we built, and it wasn’t really there in the building of it. The idea of variable abstraction from terms is all we used, and we only used it during the formation of the AST.
Parsing simple sentences in Prolog, you get grammars that look kind of like this:
sentence --> np, vp.
np --> pronoun.
np --> noun.
vp --> iv.
vp --> tv.
pronoun --> [i].
noun --> [cheese].
iv --> [sit].
tv --> [like], np.Now with this, it’s possible to parse sentences as complex and interesting as “i like cheese” or “i sit”. Wow! Except, just accepting them is not very interesting:
| ?- phrase(sentence, [i, like, cheese]).
true The computer scientist will want to actually obtain the parse tree, which is going to have the same structure as the grammar:
sentence(s(NP,VP)) --> np(NP), vp(VP).
np(pronoun(P)) --> pronoun(P).
np(noun(N)) --> noun(N).
vp(iv(IV)) --> iv(iv(IV)).
vp(tv(TV, NP)) --> tv(TV), np(NP).
pronoun(i) --> [i].
noun(cheese) --> [cheese].
iv(sit) --> [sit].
tv(like) --> [like].This gives us a parse tree:
| ?- phrase(sentence(S), [i, like, cheese]).
S = s(pronoun(i),tv(like,noun(cheese))) However, the result is hostile to evaluation. Why should the rest of my program have to know everything about my grammar? We should insulate it with a nice intermediate representation—and we’re using Prolog, so let’s make that intermediate representation look more like a Prolog query! likes(i, cheese)!
Wait a second. For this to work, I need to return a functor likes/2, but I don’t have likes/2 until after I parse i. And, I have to put cheese in there after parsing likes! This tree has a totally different shape than the input!
The solution turns out to be:
- Use a lambda calculus-styled function as the verb phrase
- Apply the noun phrases to that verb phrase to produce the result
In other words, our verb produced by our vp//1 isn’t going to be likes/2, it’s going to be a lambda expression which, when applied to the subject, produces that likes/2 functor. It’s going to be λx.likes(x,cheese). In Prolog, we’re going to encode this as X^likes(X, cheese), and then we can have a reduction step that looks like reduce(X^Term, X, Term):
| ?- reduce(X^likes(X,cheese),i,T).
T = likes(i,cheese)
X = iSo round three:
reduce(X^Term, X, Term).
sentence(S) --> np(NP), vp(VP), { reduce(VP, NP, S) }.
np(P) --> pronoun(P).
np(N) --> noun(N).
vp(IV) --> iv(IV).
vp(VP) --> tv(TV), np(NP), { reduce(TV, NP, VP) }.
pronoun(i) --> [i].
noun(cheese) --> [cheese].
iv(X^sits(X)) --> [sit].
tv(X^Y^likes(Y,X)) --> [like].Note that we flipped the variables around in likes/2 because the next thing in the parse tree is the direct object, so that will be the first reduction, and the subject (which we obtained before) is going to get applied last, when the whole parse is complete. And the result?
| ?- phrase(sentence(S), [i,like,cheese]).
S = likes(i,cheese) Groovy. But… it turns out that reduce operator is so simple, we can do what it does without calling it explicitly. Ready?
sentence(S) --> np(NP), vp(NP^S).
np(P) --> pronoun(P).
np(N) --> noun(N).
vp(IV) --> iv(IV).
vp(TV) --> tv(NP^TV), np(NP).
pronoun(i) --> [i].
noun(cheese) --> [cheese].
iv(X^sits(X)) --> [sit].
tv(X^Y^likes(Y,X)) --> [like].Kind of spooky looking, seeing np(NP), vp(NP^S), but it still works, because the structure that vp//1 produces is going to look like X^foo(...,X,...) for some term and saying NP^S is going to force NP and X to be equal, which is evaluation the way lambda calculus does it. Proof it works:
| ?- phrase(sentence(S), [i,like,cheese]).
S = likes(i,cheese) This is cool. But it turns out most noun phrases are not atoms like i, but actually they work out to be variables with quantifiers. The most obvious is a sentence like “a student wrote a program”, which should not parse into wrote(student, program) but instead something more complex…